Πρακτικό μάθημα 9 υπολογισμός παραγώγων. Πρακτικό μάθημα "υπολογισμός παραγώγων"

Πρακτικό μάθημα

Θέμα:Εύρεση παραγώγων. Εφαρμογή της παραγώγου στη μελέτη συνάρτησης και γραφική παράσταση.

Στόχος: Κατακτήστε τον υπολογισμό των παραγώγων, μάθετε να εξερευνάτε μια συνάρτηση χρησιμοποιώντας μια παράγωγο

Μέσα εκπαίδευσης:τετράδια για πρακτικές ασκήσεις, παρουσιάσεις για το θέμα, πόροι του Διαδικτύου.

1. Εξετάστε το θεωρητικό υλικό για τα θέματα: «Κανόνες υπολογισμού παραγώγων», «Ακρότατο συνάρτησης», «Κυρτότητα, κοιλότητα. Σημείο καμπής.

2. Εξετάστε δείγματα εργασιών.

3. Ολοκληρώστε την δοκιμαστική εργασία Νο.1.

Ερωτήσεις τεστ:

1. Ορίστε το μέγιστο (ελάχιστο) μιας συνάρτησης σε ένα σημείο. Τι μπορεί να ειπωθεί για το πρόσημο της αύξησης της συνάρτησης σε μια αρκετά μικρή γειτονιά του μέγιστου (ελάχιστου) σημείου;

2. Ποιες είναι οι απαραίτητες προϋποθέσεις για την ύπαρξη ακρότατου συνάρτησης; Ποια είναι η γεωμετρική τους σημασία;

3. Ποιος είναι ο κανόνας για την εύρεση της μεγαλύτερης και της μικρότερης τιμής μιας συνάρτησης σε ένα τμήμα;

4. Καθορίστε την κυρτότητα (κοιλότητα) της καμπύλης στο διάστημα.

5. Ποιος είναι ο κανόνας για την εύρεση διαστημάτων κυρτότητας και κοιλότητας μιας καμπύλης;

6. Σημείο καμπύλης. Πώς να το βρείτε;

7. Ποιος είναι ο αλγόριθμος για τη γραφική παράσταση μιας συνάρτησης;

Κανόνες υπολογισμού παραγώγων

Παράγωγος μιγαδικής συνάρτησης.

Αν ένα στο=ƒ( και), u=φ(x), τότε στο¢ ( Χ)=ƒ¢ (u) φ¢ (Χ).

Παράγωγο αθροίσματος.

Αν ένα στο(Χ)=και(Χ)+v (Χ), έπειτα στο¢ (Χ)=και¢ (Χ)+v ¢ (Χ)

Παράγωγο του προϊόντος.

Αν ένα y(x)=u(Χ)· v (Χ), έπειτα στο¢ = και¢ · v + u · v ¢ .

Συγκεκριμένα, ( Με· και)¢ =γ· και¢ , δηλαδή, ο σταθερός παράγοντας αφαιρείται κάτω από το πρόσημο της παραγώγου. Είναι εύκολο να το επαληθεύσετε

(u 2 ) ¢ = 2 u u ¢ , (ου 3 ) ¢ =3u 2 u ¢ , … , (υ n ) ¢ =n u n–1 u ¢ .

παράγωγο του πηλίκου.

Αν τότε
.

Πίνακας παραγώγων

1. (Με)¢ =0

Για μια σύνθετη συνάρτηση: αν u=u(x), έπειτα:

2. (Χ)¢ =1

3. (Χ α )¢ = α · Χα–1, έναείναι οποιοσδήποτε πραγματικός αριθμός.

.

3.

4. (ένα Χ ) ¢ =α Χ · ln ένα

4.

5. (κούτσουρο ένα Χ) ¢ =

.

5.

6. (sinx)¢ =cos x

6.

7. (συν x)¢ = -αμαρτία x

7.

8. (tgx)¢ =

8.

9. (ctgx)¢ =

9.

10.

10.

11.

11.

12.

12.

13.

13.

Εξετάστε παραδείγματα

Παράδειγμα 1

y=(3–2 αμαρτία 5χ ) 4 | Εφαρμόζουμε παραγώγους τύπους για και α , αμαρτία u |

y ¢ =4 (3–2 sin5x) 3 (3–2sin5x) ¢ =4 (3–2 sin5x) 3 (0–2 cos5x 5) = –40 (3–2 sin5x) 3 .

Παράδειγμα 2

.

Παράδειγμα 3

.

Παράδειγμα 4

Παράδειγμα 5

.

Λειτουργία ακραία

Η μελέτη μιας συνάρτησης σε ένα άκρο είναι μια από τις πιο σημαντικές εφαρμογές των παραγώγων. Εξετάστε τον ορισμό των ελάχιστων και μεγίστων και πώς να τα βρείτε.

Αφήστε τη συνάρτηση ƒ( Χ) ορίζεται και διαφοροποιείται σε κάποιο σύνολο και το σημείο ΧΤο 0 είναι ένα σημείο μέσα του.

Ορισμός.Λειτουργία ƒ (Χ) στο σημείο Χ 0 έχει το μέγιστο(ελάχιστο) αν υπάρχει τέτοια γειτονιά του σημείου Χ 0 , που είναι για όλους Χαπό αυτή την περιοχή ƒ (Χ) < ƒ (Χ 0 ) (ƒ (Χ) > ƒ (Χ 0 )).

Τελεία ΧΤο 0 ονομάζεται τότε σημείο το μέγιστο(ελάχιστο).

Ρύζι. ένας.

Εμφανίζεται ένα γράφημα μιας συνάρτησης που έχει δύο μέγιστα σημεία ( Χ 1 και Χ 3) και δύο ελάχιστες μονάδες ( Χ 2 και Χ 4), και η μέγιστη τιμή μπορεί να είναι μικρότερη από την ελάχιστη ( ƒ (Χ 1 ) < ƒ (Χτέσσερα)). Αυτό τονίζει το γεγονός ότι χαρακτηρίζουμε την ιδιομορφία της συνάρτησης μόνο κοντά σε κάποιο σημείο.

Οι τιμές της συνάρτησης στα σημεία μέγιστου και ελάχιστου ονομάζονται ακραίες τιμές ή άκρα. Το παραπάνω γράφημα δείχνει ότι τα ακραία σημεία ( Χ 1 , Χ 2 , Χ 3 , Χ 4) προσδιορίστε τα διαστήματα μονοτονίας της συνάρτησης, σε καθένα από τα οποία η παράγωγος διατηρεί ένα ορισμένο πρόσημο. Σε ακραία σημεία, φυσικά, το παράγωγο εξαφανίζεται. Ας διατυπώσουμε ένα θεώρημα για απαραίτητη προϋπόθεση την ύπαρξη ακραίου.

Θεώρημα.Εάν η συνάρτηση ƒ (Χ) στο σημείο ΧΤο 0 έχει ένα άκρο, τότε η παράγωγος της συνάρτησης σε αυτό το σημείο είναι ίση με μηδέν, δηλαδή ƒ¢ ( Χ 0)=0.

Σημειώνουμε αμέσως ότι αυτή η συνθήκη δεν είναι επαρκής, δηλ. η αντίστροφη πρόταση δεν είναι πάντα αληθής. Από την ισότητα ƒ ¢ ( Χ 0)= Το 0 δεν ακολουθεί απαραίτητα αυτό στο σημείο Χ 0 υπάρχει ακρότητα.

Αυτό επιβεβαιώνεται από ένα παράδειγμα με τη συνάρτηση ƒ (Χ)=x 3 .

Ας βρούμε ƒ ¢ ( Χ)= 3Χ 2 . Στο σημείο Χ=0 ƒ ¢(0)=0 . Αλλά αυθαίρετα κοντά στην ουσία Χ=0 εύρεση Χ> 0, όπου ƒ (Χ)=x 3 > 0, εύρημα Χ< 0, где ¦ (Χ)=Χ 3 < 0. Т. е. не существует какая-либо малая окрестность точки Χ=0, όπου για όλους Χτιμή συνάρτησης στο σημείο ΧΤο =0 θα είναι το μεγαλύτερο ή το μικρότερο. Ως εκ τούτου, το σημείο ΧΤο =0 δεν είναι ακραίο σημείο.

Μπορείτε να διαφωνήσετε διαφορετικά. Αφού το παράγωγο ƒ ¢ (x)=3x 2 , μετά η συνάρτηση ƒ(x)=x 3 αυξάνεται για κάθε πραγματικό x και δεν έχει άκρα.

Τα σημεία όπου απαραίτητη προϋπόθεσηακραίο (ƒ ¢ (x)=0)που ονομάζεται κρίσιμος .

Προφανώς, η εφαπτομένη στη γραφική παράσταση της συνάρτησης στα σημεία όπου ƒ ¢ (x)=0,παράλληλα με τον άξονα της τετμημένης Οξ .

Επαρκής κατάστασηακραίο δίνεται στα ακόλουθα θεωρήματα.

Θεώρημα 1.Αν ένα ΧΤο 0 είναι το κρίσιμο σημείο της συνάρτησης, και όταν τη διέρχεται, η παράγωγος αλλάζει πρόσημο, τότε Χ 0 - ακραίο σημείο, δηλαδή, εάν η παράγωγος αλλάζει σημάδι από συν σε πλην - το μέγιστο σημείο, εάν - από μείον στο συν - το ελάχιστο σημείο.

Σημειώστε ότι δεν υπάρχει ακρότατο σε ένα σημείο εάν η παράγωγος δεν αλλάξει πρόσημο. Ο κανόνας για τη μελέτη του ακραίου με χρήση της πρώτης παραγώγου είναι γνωστός από το σχολικό μάθημα. Μερικές φορές είναι πιο βολικό να διαμορφωθεί μια επαρκής συνθήκη για ένα άκρο χρησιμοποιώντας τη δεύτερη παράγωγο.

Αφήστε τη συνάρτηση ƒ( Χ) είναι δύο φορές διαφοροποιήσιμο σε κάποιο τομέα (δηλαδή, ƒ( Χ) έχει ƒ¢ ( Χ) και ƒ ¢¢ ( Χ)).

Θεώρημα 2.Αν ένα Χ 0 - κρίσιμο σημείο της συνάρτησης ƒ(x)και ƒ ¢¢ (Χ 0 ) > 0 , έπειτα Χ 0 είναι το ελάχιστο σημείο, αν ƒ ¢¢ (Χ 0 ) < 0, то ΧΤο 0 είναι το μέγιστο σημείο.

Με τη βοήθεια της δεύτερης παραγώγου προσδιορίζεται η κυρτότητα ή η κοιλότητα της γραφικής παράστασης της συνάρτησης.

Κυρτότητα, κοιλότητα. Σημείο καμπής.

Καμπύλη y=ƒ(Χ) λέγεται κυρτόςου παρακάτωοποιαδήποτε από αυτήν εφαπτομένος

ƒ ¢¢ ( Χ) < 0.

Καμπύλη y=ƒ(Χ) λέγεται κοίλος σε ένα διάστημα εάν όλα τα σημεία της καμπύλης βρίσκονται πάνω από οποιαδήποτε από αυτήν εφαπτομένος σε αυτό το διάστημα. Στη συνέχεια σε αυτό το διάστημα

ƒ ¢¢(x) > 0

Ορισμός. σημείο καμπής Η καμπύλη είναι ένα σημείο στο οποίο η καμπύλη είναι κυρτή στη μία πλευρά και κοίλη στην άλλη.

Στο σημείο της καμπής ƒ ¢¢ ( Χ)=0.

Άρα, το πρόσημο της δεύτερης παραγώγου (καθώς και το πρόσημο της ίδιας της συνάρτησης και της πρώτης παραγώγου της) υποδηλώνει τα χαρακτηριστικά της γραφικής παράστασης της συνάρτησης. Ας τα ξαναδούμε.

Αν για όλους Χστο μεσοδιάστημα ( ένα, σι) ƒ (Χ) > 0 (ƒ (Χ) < 0), τότε το γράφημα βρίσκεται πάνω (κάτω) από τον άξονα x.

Αν για όλους Χστο μεσοδιάστημα ( ένα, σι) ƒ ¢ ( Χ) > 0 (ƒ ¢ ( Χ) < 0), то функция на (ένα, σι) αυξάνει (μειώνεται).

Αν για όλους Χστο μεσοδιάστημα ( ένα, σι) ƒ ¢¢ ( Χ) > 0 (ƒ ¢¢ ( Χ) < 0), то график на (ένα, σι) είναι κοίλο (κυρτό).

Εξίσωση ƒ( Χ)=0 ορίζει τα «μηδενικά» της συνάρτησης, δηλαδή τα σημεία τομής του γραφήματος με τον άξονα Ox.

Η εξίσωση ƒ ¢ ( Χ)=0 ορίζει κρίσιμα σημεία.

Η εξίσωση ƒ ¢¢ ( Χ)=0 ορίζει πιθανά σημεία καμπής.

Σχέδιο Μελέτης Συναρτήσεων

Να μελετήσει τη συνάρτηση ƒ (Χ) και σχεδίαση y=ƒ(Χ) πρέπει να βρεθεί:

1) την περιοχή ορισμού της συνάρτησης και τα σημεία τομής του γραφήματος με τους άξονες συντεταγμένων.

2) διαστήματα μονοτονίας.

3) ακραία σημεία και τιμές συνάρτησης σε αυτά τα σημεία.

4) διαστήματα κυρτότητας και κοιλότητας του γραφήματος.

5) σημεία καμπής γραφήματος.

6) χτίστε στο καρτεσιανό σύστημα συντεταγμένων όλα τα ληφθέντα σημεία (μερικές φορές, για να διευκρινίσετε το γράφημα, να λάβετε επιπλέον σημεία) και το ίδιο το γράφημα.

Οι μικρότερες και μεγαλύτερες τιμές μιας συνάρτησης σε ένα τμήμα

Κατά την επίλυση ορισμένων προβλημάτων της μεθόδου βελτιστοποίησης, είναι σημαντικό να μπορείτε να βρείτε τις μικρότερες ή μεγαλύτερες τιμές μιας συνάρτησης σε ένα συγκεκριμένο διάστημα. Η συνάρτηση φτάνει σε αυτές τις τιμές είτε σε κρίσιμα σημεία είτε στα άκρα του τμήματος.

Σχέδιο αναζήτησηςτις μικρότερες και μεγαλύτερες τιμές της συνάρτησης ƒ (Χ) στο τμήμα [ ένα, σι].

1. Να βρείτε την παράγωγο μιας συνάρτησης ƒ ¢ ( Χ).

2. Βρείτε κρίσιμα σημεία από την εξίσωση ƒ ¢ ( Χ)=0.

3. Επιλέξτε εκείνα τα κρίσιμα σημεία που ανήκουν στο δεδομένο τμήμα [ ένα, σι] και βρείτε την τιμή της συνάρτησης ƒ (Χ) σε κάθε τέτοιο σημείο.

4. Υπολογίστε τις τιμές συνάρτησης ƒ (Χ) στα άκρα του τμήματος: ƒ( ένα) και ƒ( σι).

5. Από τις λαμβανόμενες τιμές της συνάρτησης, επιλέξτε τη μεγαλύτερη (μεγαλύτερη) και τη μικρότερη (μικρότερη).

Παράδειγμα 2

Βρείτε τις μεγαλύτερες και τις μικρότερες τιμές μιας συνάρτησης ƒ(x)=Χ 3 -9x 2 +24х–10στο τμήμα.

1. ƒ ¢ ( Χ)= 3Χ 2 – 9 2 Χ 2 + 24.

2. ƒ ¢ ( Χ)=0, 3(Χ 2 –6Χ+8)=0, Χ 1 =2, Χ 2 =4.

3. Το σημείο x 2 \u003d 4 δεν ανήκει στο τμήμα. Επομένως, υπολογίζουμε την τιμή της συνάρτησης μόνο στο σημείο Χ 1 =2

ƒ(2)=2 3 –9 2 2 +24 2–10=10.

4. Τιμές συναρτήσεων στα άκρα του τμήματος: ƒ(0)= –10, ƒ(3)=3 3 –9 3 2 +24 3–10, ƒ(3)=8.

5. Ληφθείσες τιμές:

ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.

Υψηλότερη τιμήισούται με 10 και επιτυγχάνεται στο σημείο Χ=2. Το μικρότερο είναι -10 και φτάνει στο σημείο Χ=0.

Παράδειγμα 3

Να βρείτε τα διαστήματα κυρτότητας και κοιλότητας και τα σημεία καμπής της καμπύλης y=x+36Χ 2 –2Χ 3 –Χ 4 .

Το πεδίο ορισμού αυτής της συνάρτησης είναι το σύνολο όλων των πραγματικών αριθμών, δηλ. ΧЄ(–∞, +∞).

Ας βρούμε τη δεύτερη παράγωγο.

στο¢=1+72 Χ–6Χ 2 –4Χ 3 .

στο¢¢=72–12 Χ–12Χ 2 = –12(Χ 2 +Χ–6).

Από την εξίσωση στο¢¢ =0 παίρνουμε την τετμημένη του σημείου καμπής:

–12(Χ 2 +Χ–6)=0 Χ 1 = –3; Χ 2 =2.

Ας ορίσουμε το σημάδι στο¢¢ σε διαστήματα

(–∞; –3), (–3; 2), (2, +∞).

Χ

(–∞, –3)

(–3; 2)

(2; +∞)

στο¢¢

σχήμα καμπύλης

κυρτός

κλίση

κοίλος

κλίση

κυρτός

Βρείτε τις τεταγμένες των σημείων καμπής:

στο(–3)=726; Μ 1 (–3; 726) – σημείο καμπής

στο(2)=114; Μ 2 (2; 114) – σημείο καμπής.

Στο διάστημα (–3; 2), η καμπύλη είναι κοίλη. Στα διαστήματα (–∞; –3) και (2; +∞), είναι κυρτό.

Καθήκοντα

Εργασία αριθμός 1.

Βρείτε σημεία διακοπής μιας συνάρτησης και κατασκευάστε ένα γράφημα

Λειτουργία ƒ (Χ) ορίζεται για όλα τα πραγματικά Χκαι είναι συνεχής σε καθένα από τα υποδεικνυόμενα διαστήματα: (–∞; –1), [–1; 0], (0, +∞). Εξερεύνηση της συνάρτησης ƒ (Χ) στη συνέχεια σε σημεία Χ= –1 και Χ=0.

Για να γίνει αυτό, σε καθένα από αυτά τα σημεία βρίσκουμε μονόπλευρα όρια.

Αφού τα μονόπλευρα όρια είναι διαφορετικά, λοιπόν Χ = –1 – σημείο ασυνέχειας πρώτου είδους.

Τα μονόπλευρα όρια είναι ίσα, δηλαδή στο σημείο x = 0 υπάρχει ένα όριο της συνάρτησης και

Ας συγκρίνουμε αυτό το όριο με την τιμή της συνάρτησης στο σημείο:

Επειδή
μετά μέσα σημείο x=0, η συνάρτηση ƒ(x) είναι συνεχής.

Ας σχεδιάσουμε τη συνάρτηση ƒ (Χ), δεδομένου ότι

1)
- εξίσωση ευθείας γραμμής,

2)
- η εξίσωση του άνω ημικυκλίου
με κέντρο την αρχή και την ακτίνα, ίσο με ένα, και υπό τον όρο –1 £ Χ£ 0 εξίσωση
ορίζει το ένα τέταρτο του κύκλου.

3) για Χ > 0 η γραφική παράσταση δίνεται από την εξίσωση
. Βρίσκουμε τα σημεία τομής αυτής της καμπύλης με τον άξονα Ox από την εξίσωση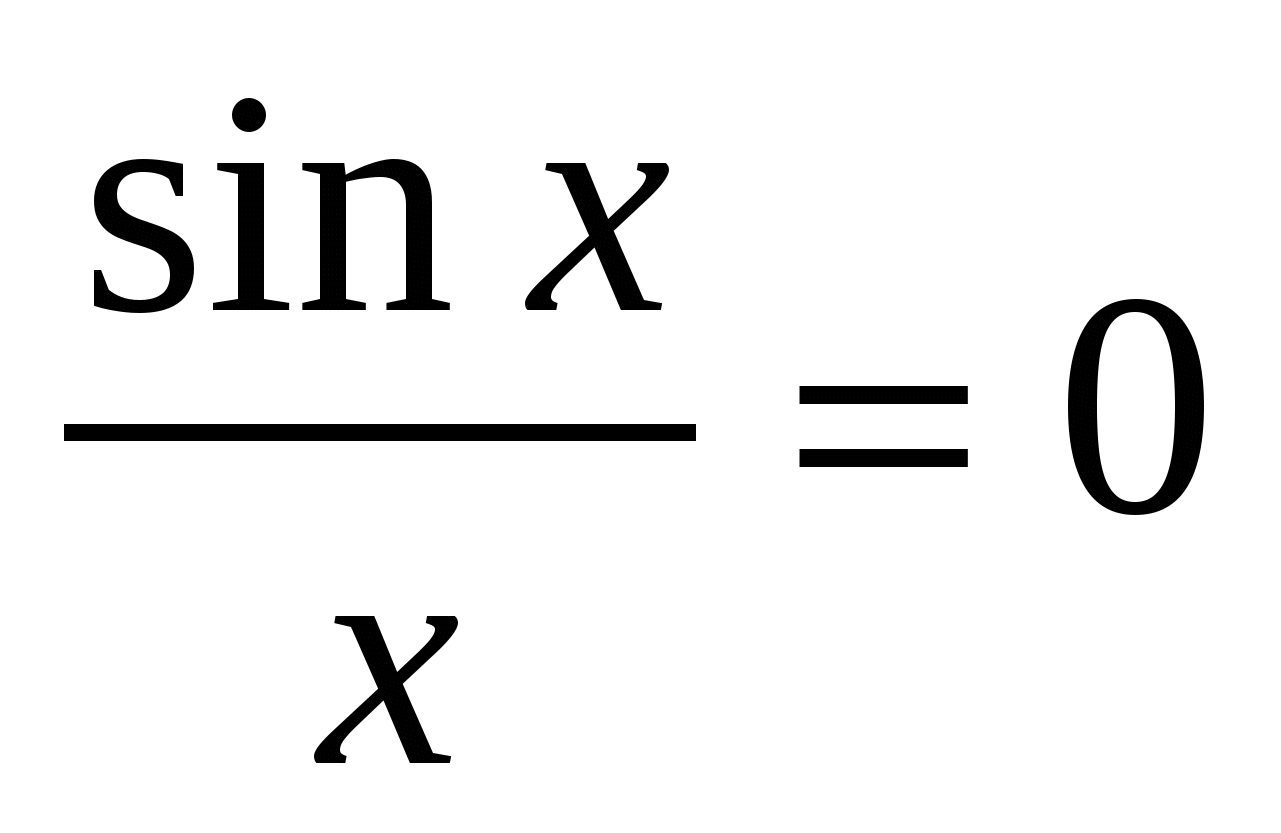
για x > 0. x= π n, όπου n =1, 2, 3, 4,

Ρύζι. 2.

Εργασία αριθμός 2.

Να συνθέσετε εξισώσεις των εφαπτομένων σε μια ευθεία
στα σημεία όπου Χ=0 και Χ=4. Να βρείτε το σημείο τομής των εφαπτομένων και τη γωνία μεταξύ τους. Κάντε ένα σχέδιο.

Εξίσωση εφαπτομένης γραμμής y=ƒ(x)έχει τη μορφή

όπου στο 0 =ƒ( Χ 0).

Στο σημείο Χ=0 στο(0)=ƒ(0)=5.

στο¢ =ƒ ¢ (Χ)=Χ–3 ƒ¢ (0)= –3.

ΜΤο 1 (0, 5) έχει τη μορφή y- 5= –3(Χ-0) ή

y= –3Χ+5.

Στο σημείο Χ=4 στο(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.

Εφαπτομένη εξίσωση σε ένα σημείο ΜΤο 2 (4, 1) έχει τη μορφή y- 1=Χ-4 ή

y=x–3.

Λαμβάνουμε το σημείο τομής των εφαπτομένων λύνοντας το σύστημα

Σημείο τομής Μ 3 (2, –1).

Γωνία φ μεταξύ των εφαπτομένων βρίσκουμε από τον τύπο:

,

όπου κ 1 = –3; κ 2 =1 – συντελεστές κλίσης εφαπτομένων.

.

Γωνία φ = arctg 2.

Ας φτιάξουμε αυτή τη γραμμή
είναι μια παραβολή με κορυφή στο σημείο όπου Χ=3, γιατί στο¢ =0 στο Χ=3. Ας βρούμε
. Τελεία Μ 4 (3; ) είναι η κορυφή της παραβολής.

R

είναι. 3.

Εργασία αριθμός 3.

Λειτουργία εξερεύνησης
και σχεδιάστε το.

1. Αυτή η συνάρτηση είναι πολυώνυμο (μπορείτε να ανοίξετε τις αγκύλες, παίρνουμε ένα πολυώνυμο τρίτου βαθμού), άρα ορίζεται, συνεχής και διαφοροποιήσιμη για οποιαδήποτε Χ.

2. Βρείτε την παράγωγο.

.

Από την εξίσωση στο¢ =0 βρείτε κρίσιμα σημεία: 3 Χ·( Χ–2)=0, Χ 1 =0, Χ 2 =2.

Ας τα εξερευνήσουμε.

Χ

(–∞, 0)

(0; 2)

(2; +∞)

στο ¢

στο

3. Άρα, η συνάρτηση αυξάνεται στα διαστήματα (–∞, 0) και (2, +∞), μειώνεται στο διάστημα (0; 2), έχει μέγιστο στο x=0 και ελάχιστο στο x=2:

στο μέγ.= στο(0)=4; στο min = στο(2)=0.

4. Να βρείτε τη δεύτερη παράγωγο.

στο¢¢ = 6 ( Χ-1).

Η καμπύλη είναι κυρτή όπου στο¢¢ < 0, т. е. 6·(Χ–1) < 0, Χ < 1.

Η καμπύλη είναι κοίλη όπου στο¢¢ > 0, δηλ. Χ > 1.

Άρα, στο διάστημα (–∞, 1) η καμπύλη είναι κυρτή. και στο διάστημα (1, +∞) είναι κοίλο.

5. Βρείτε το σημείο καμπής από την εξίσωση στο¢¢ =0. Με αυτόν τον τρόπο, Χ=1 είναι η τετμημένη του σημείου καμπής, αφού αυτό το σημείο χωρίζει τα διαστήματα κυρτότητας και κοιλότητας της καμπύλης. Τετταγμένη σημείου καμπής: στο(1)=2.

Γράφημα συνάρτησης στο=(Χ+1)( Χ–2) Το 2 διασχίζει τον άξονα x στο στο=0, δηλαδή στο Χ= –1 και Χ=2;

διασχίζει τον άξονα y Χ=0, δηλαδή στο στο=4. Πήραμε τρεις βαθμούς: (-1; 0), (2; 0), (0; 4). Όλοι οι βαθμοί που αποκτήθηκαν θα εισαχθούν στον πίνακα προσθέτοντας γειτονικούς.

–2

–1

–16

R

είναι. 4 Καμπύλη y=(x+1)(x–2) 2 .

Εργασία αριθμός 1

Προσφέρονται στην προσοχή σας εργασίες στις οποίες μπορεί να υπάρχουν μία, δύο, τρεις ή περισσότερες σωστές απαντήσεις. Κυκλώστε τους αριθμούς όλων των σωστών απαντήσεων

1. Αν
τότε η συνάρτηση

1) αύξηση

2) μειώνεται

3) σταθερό

2. Αν

1) Αύξηση

2) Φθίνουσα

3. Αν
, μετά η συνάρτηση

1) Αύξηση

2) Φθίνουσα

4. Αν
, μετά η συνάρτηση

1) Αύξηση 3) Φθίνουσα

2) Σταθερά 4) Μονοτονικά

5. Λειτουργία
Είναι

1) Ακόμη

2) ούτε καν

3) ούτε ζυγός ούτε περιττός

4) Περιοδική

5) Όχι περιοδική

6) Τριγωνομετρικό

7) Δημοτικό

6. Λειτουργία
Είναι

1) ακόμη και

2) περίεργο

3) ούτε ζυγός ούτε περιττός

4) περιοδική

5) όχι περιοδική

6) τριγωνομετρική

7) στοιχειώδες

2) Weierstrass 4) Dirichlet 6) Leibniz

8) Απόφαση
Εξισώσεις

1) 0 3) 0 και 3 5) 2 7) 3

2) 2 και 3 4) 2 6) -5 και 1 8) 5 και 1

9) λύση ανισότητας

1) (; 1) 3) (; 1) 5) (-;1)

2) (1; 5) 4) (2; ) 6)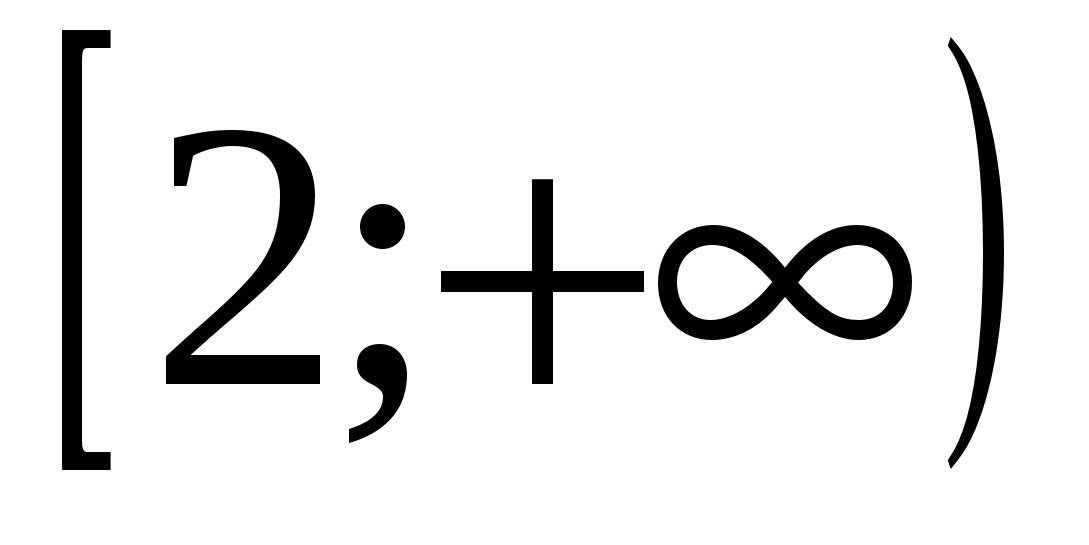

10) Μέθοδος
Είναι το άθροισμα

1) διανύσματα

2) άμεσος

3) αποκόπηκε

11) Αν
, μετά η συνάρτηση

1) Κοίλη 3) Κυρτή 5) Φθίνουσα

2) Μονοτονική 4) Αύξουσα 6) Σταθερή

12) το εύρος της συνάρτησης είναι

1) (;0)

2) (0; )

3) (-;)

4) (0;1)

5)

6)

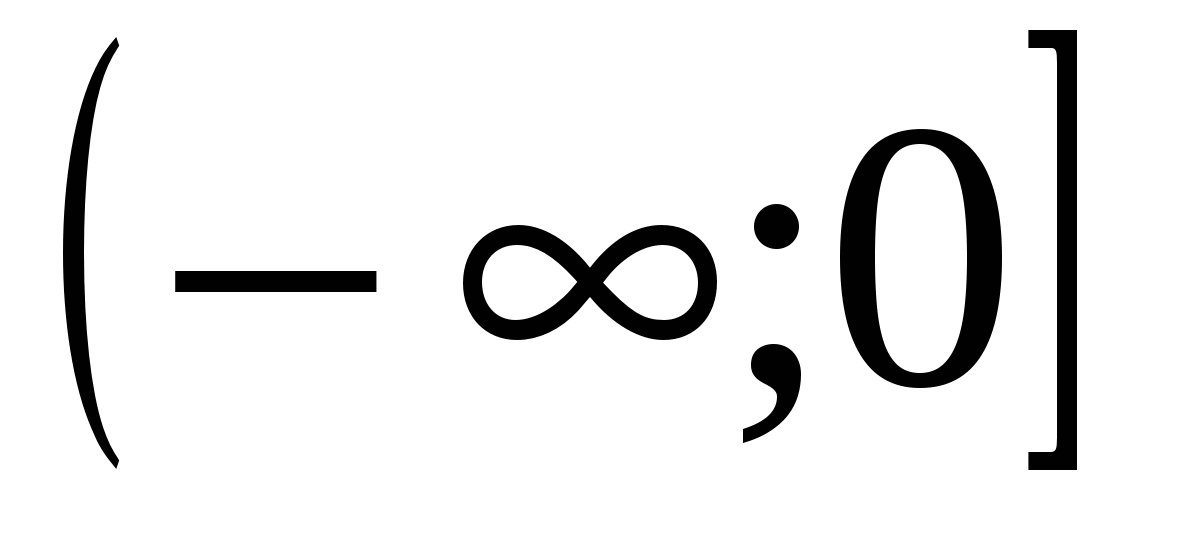
7) (-1;1)

8)

9)

13) λειτουργία
είναι

1) ενδεικτικά

2) τριγωνομετρική

3) δύναμη

4) λογαριθμική

14) αν συναρτήσεις y= Χ τότε αυτή είναι

1) ακόμη και

2) περίεργο

3) ούτε ζυγός ούτε περιττός

15) λειτουργία
στο
είναι

Πρακτική δουλειά

μαθηματικά

1. Εύρεση του ορίου μιας συνάρτησης. Το πρώτο και το δεύτερο υπέροχα όρια.

2. Παράγωγος μιγαδικής συνάρτησης. Διερεύνηση της συνάρτησης μιας μεταβλητής και σχεδίαση.

3. Δοκιμή«Η Εφαρμογή του Διαφορικού Λογισμού στη Μελέτη των Συναρτήσεων».

4. Εύρεση αόριστων ολοκληρωμάτων. Υπολογισμός ορισμένων ολοκληρωμάτων.

5. Υπολογισμός οριζόντων.

6. Επίλυση συστημάτων γραμμικών εξισώσεων με τη μέθοδο Cramer. Δοκιμή.

7. Επίλυση προβλημάτων με θέμα «Σετ». Τύποι της άλγεβρας της λογικής.

8. Υπολογισμός των πιθανοτήτων τυχαίων γεγονότων. Τύπος Συνολικών Πιθανοτήτων.

9. Υπολογισμός αριθμητικών χαρακτηριστικών.

10. Δοκιμαστική εργασία «Βασικές αρχές Θεωρίας Πιθανοτήτων και Μαθηματική Στατιστική»

11. Τριγωνομετρική μορφή μιγαδικού αριθμού.

12. Πράξεις με μιγαδικούς αριθμούς σε διάφορες μορφές.

ΜΕΘΟΔΟΛΟΓΙΚΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΠΡΑΚΤΙΚΕΣ ΕΡΓΑΣΙΕΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ

2 ΠΟΡΕΙΑ

Το πρακτικό μάθημα είναι μια μορφή οργάνωσης της εκπαιδευτικής διαδικασίας, που περιλαμβάνει την εκτέλεση από τους μαθητές κατόπιν ανάθεσης και υπό την καθοδήγηση ενός δασκάλου μιας ή περισσότερων πρακτικών εργασιών.

Έτσι, στα πρακτικά μαθήματα στα μαθηματικά, οι μαθητές αναπτύσσουν την ικανότητα επίλυσης προβλημάτων, τα οποία στο μέλλον θα πρέπει να χρησιμοποιηθούν για την επίλυση επαγγελματικών προβλημάτων σε ειδικούς κλάδους.

Κατά τη διάρκεια της πρακτικής εργασίας, οι μαθητές κατακτούν την ικανότητα χρήσης πηγών πληροφοριών, εργασίας με κανονιστικά έγγραφακαι εκπαιδευτικό υλικό, βιβλία αναφοράς, πραγματοποιήστε σχέδια, διαγράμματα, πίνακες, λύστε διαφορετικό είδοςεργασίες, κάντε υπολογισμούς.

Εργασίες που λύνονται κατά τη διάρκεια πρακτικών μαθημάτων στα μαθηματικά:

1) επέκταση και εδραίωση της θεωρητικής γνώσης στα μαθηματικά που αποκτήθηκαν κατά τη διάρκεια των διαλέξεων.

2) ο σχηματισμός των πρακτικών δεξιοτήτων και ικανοτήτων των μαθητών που είναι απαραίτητες για την επιτυχή επίλυση προβλημάτων στα μαθηματικά.

3) ανάπτυξη στους μαθητές της ανάγκης για αυτοεκπαίδευση και βελτίωση των γνώσεων και των δεξιοτήτων στη διαδικασία της μελέτης των μαθηματικών.

4) η διαμόρφωση μιας δημιουργικής στάσης και ερευνητική προσέγγισηστη διαδικασία της μελέτης των μαθηματικών.

5) ο σχηματισμός επαγγελματικά σημαντικών ιδιοτήτων του μελλοντικού ειδικού και οι δεξιότητες εφαρμογής της αποκτηθείσας γνώσης στον επαγγελματικό τομέα.

Πρακτικό μάθημα νούμερο 1.Υπολογισμός ορίων συναρτήσεων. Το πρώτο και το δεύτερο υπέροχα όρια.

Θέμα : Υπολογισμός ορίων συναρτήσεων.

Στόχος: απόκτηση βασικών γνώσεων στον τομέα των θεμελιωδών ενοτήτων των μαθηματικών . Έλεγχος της αφομοίωσης της γνώσης για τον υπολογισμό των ορίων των συναρτήσεων. Επαναλάβετε και συστηματοποιήστε τη γνώση για αυτό το θέμα.

Καθήκοντα:

Ανάπτυξη δημιουργικής επαγγελματικής σκέψης.

Κατοχή της γλώσσας της επιστήμης, δεξιότητες στη λειτουργία με έννοιες.

Κατακτήστε τις δεξιότητες και τις ικανότητες στον καθορισμό και την επίλυση προβλημάτων.

Εμβάθυνση της θεωρητικής και πρακτικής κατάρτισης.

Ανάπτυξη πρωτοβουλίας και ανεξαρτησίας των μαθητών.

Ενοποίηση υπολογιστικών δεξιοτήτων.

Συνεχίστε να εργάζεστε στη μαθηματική ομιλία.

Διαμόρφωση δεξιοτήτων ανεξάρτητης εργασίας, εργασία με σχολικό βιβλίο, δεξιότητες ανεξάρτητης απόκτησης γνώσεων.

Ανάπτυξη της ικανότητας να επισημάνετε το κύριο πράγμα κατά την εργασία με κείμενο.

Διαμόρφωση ανεξαρτησίας σκέψης, νοητικές λειτουργίες: σύγκριση, ανάλυση, σύνθεση, γενίκευση, αναλογία.

Δείξτε στους μαθητές το ρόλο της συστηματικής εργασίας για να εμβαθύνουν και να βελτιώσουν τη δύναμη της γνώσης, την κουλτούρα της ολοκλήρωσης των εργασιών.

Ανάπτυξη δημιουργικότηταΦοιτητές.

Παροχή πρακτικής εργασίας:

Θεωρητικό υλικό μεθοδολογικών συστάσεων για πρακτική εργασία.

Μαθηματικά, - Σειρά: Δευτεροβάθμια επαγγελματική εκπαίδευση. - Rostov-on-Don "Phoenix", σελ.

Η πορεία της πρακτικής συνεδρίας.

1. Διατύπωση του θέματος του μαθήματος, επεξήγηση της σύνδεσης του θέματος με άλλα θέματα του ακαδημαϊκού κλάδου.

2.Έλεγχος της ετοιμότητας των μαθητών για το μάθημα.

3. Διεξαγωγή μαθήματος απευθείας σύμφωνα με το αντικείμενο και σύμφωνα με το πρόγραμμα εργασίας του κλάδου:

Να μελετήσει το θεωρητικό υλικό με θέμα «Υπολογισμός ορίων συναρτήσεων».

Εξετάστε παραδείγματα επίλυσης τυπικών εργασιών.

Εκτελέστε ανεξάρτητη εργασία για τον υπολογισμό των ορίων των συναρτήσεων χρησιμοποιώντας το πρώτο και το δεύτερο αξιοσημείωτο όριο.

Απάντησε σε ερωτήσεις ασφαλείας.

Θεωρητικές πληροφορίες και μεθοδολογικές συστάσεις

για την επίλυση προβλημάτων.

1. Παρουσίαση θεωρητικού υλικού.

Για να υπολογίσετε το όριο μιας συνάρτησης σε ένα σημείο, χρειάζεστε:

1) Αντικαταστήστε αντί της μεταβλητής x σε τι τείνει το x.

2) Εάν μετά τη συμπλήρωση του σημείου 1) έχουμε αβεβαιότητα για τη φόρμα https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">και αντικαταστήσουμε το βέλος με μείον: (χ-α).

3) Εάν, μετά τη συμπλήρωση του σημείου 1), έχουμε αβεβαιότητα για τη φόρμα https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> , που σχετίζεται με τις τιμές των τριγωνομετρικών συναρτήσεων, πρέπει να χρησιμοποιήσουμε το πρώτο αξιοσημείωτο όριο.

Ορισμός.Το πρώτο αξιοσημείωτο όριο ονομάζεται όριο

https://pandia.ru/text/78/405/images/image007_4.png" alt="(!LANG:$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}

5) Ορισμός:Το δεύτερο αξιοσημείωτο όριοονομάζεται όριο

Ο αριθμός που δίνει αυτό το όριο παίζει πολύ σημαντικό ρόλο τόσο στη μαθηματική ανάλυση όσο και σε άλλους κλάδους των μαθηματικών. Ο αριθμός καλείται βάση φυσικών λογαρίθμων ( https://pandia.ru/text/78/405/images/image009_4.png" alt="(!LANG:$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}

2. Εμπέδωση της ύλης που μελετήθηκε.

Παράδειγμα 1

https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4

Χρησιμοποιήσαμε τον κανόνα 1) και αντικαταστήσαμε με το x αυτό για το οποίο προσπαθεί το x, δηλ. x=2.

Παράδειγμα 2

https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5

Παράδειγμα 3

https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6

Παράδειγμα 4

https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">

Παράδειγμα 5

https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2

Παράδειγμα 6

https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">

σι)

σε)

3. Εμπέδωση γνώσεων, δεξιοτήτων και ικανοτήτων.

Εκτελέστε ανεξάρτητη εργασία για τον υπολογισμό των ορίων των συναρτήσεων.

Πρακτική δουλειά №1. Επιλογή 1 Υπολογίστε το όριο συνάρτησης: 1. . 2. . 3. . 10. .

Πρακτική εργασία №1. Επιλογή 2 Υπολογίστε το όριο συνάρτησης: 1. . 2. . 3. . 10.

Πρακτική εργασία νούμερο 2.

Θέμα : Εύρεση παραγώγου συνάρτησης. Διερεύνηση της συνάρτησης μιας μεταβλητής και σχεδίαση.

Στόχος : Να ελέγξει στην πράξη τη γνώση της έννοιας της παραγώγου μιας συνάρτησης, την ικανότητα εύρεσης παραγώγων στοιχειωδών συναρτήσεων, μιγαδικών συναρτήσεων, αντίστροφων συναρτήσεων, χρησιμοποιώντας πίνακα παραγώγων και κανόνες διαφοροποίησης, την έννοια μιγαδικής και αντίστροφης συνάρτησης, την ικανότητα εφαρμογής μιας παραγώγου για τη μελέτη συναρτήσεων.

Παροχή πρακτικής εργασίας:

Σχολικό βιβλίο. «Μαθηματικά». – M.: Bustard, 2010.

Μαθηματικά. M: Forum-Infa 2008.

Ατομικές κάρτες με δυνατότητα πρακτικής εργασίας.

1. Θεωρητικό υλικό και παραδείγματα εύρεσης παραγώγου συνάρτησης.

Ορισμός:Η παράγωγος της συνάρτησης f (x) (f "(x)) στο σημείο x είναι το όριο του λόγου της αύξησης της συνάρτησης προς την αύξηση του ορίσματος όταν η αύξηση του ορίσματος τείνει στο μηδέν:

https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">

Κανόνες διαφοροποίησης.

Αν οι συναρτήσεις f(x) και g(x) έχουν παράγωγες, τότε

2. (u+v)′=u′+v′

3. (uv)′=u′v+v′u

4. (С u)′=С u′, όπου С=στ

5..png" width="49" height="54 src=">

6. Παράγωγος μιγαδικής συνάρτησης:

f′(g(x))=f′(g) g′(x)

2. Παραδείγματα.

1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).

Η συνάρτηση είναι προϊόν δύο παραγόντων: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.

Η συνάρτηση είναι ένα πηλίκο δύο παραστάσεων: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215 "height="57 src=">.png" width="197 height=36" height="36">

Λύση. Ας βρούμε την παράγωγο αυτής της συνάρτησης σύμφωνα με τον κανόνα διαφοροποίησης μιας μιγαδικής συνάρτησης (τύπος 6):

5. Αν , τότε

6. y = Χ 3 – 3Χ 2 + 5Χ+ 2. Βρείτε y "(–1).

y " = 3Χ 2 – 6Χ+ 5. Επομένως, y "(–1) = 14.

7. Αν ένα y=ln Χ cos Χ, έπειτα y" = (ln Χ) "κοσ Χ+ln Χ(συν Χ) " =1/Χ cos Χ– Ιν Χαμαρτία Χ.

Ας δοθεί μια συνάρτηση. Για να το μελετήσετε χρειάζεστε:

1) Βρείτε το πεδίο ορισμού του. Αν δεν είναι πολύ δύσκολο, τότε είναι χρήσιμο να βρείτε και το εύρος. (Ωστόσο, σε πολλές περιπτώσεις, το ζήτημα της εύρεσης αναβάλλεται μέχρι να βρεθούν τα άκρα της συνάρτησης.)

2) Μάθετε τις γενικές ιδιότητες της συνάρτησης που θα βοηθήσουν στον προσδιορισμό της συμπεριφοράς της: αν η συνάρτηση είναι άρτια ή περιττή, αν είναι περιοδική.

3) Μάθετε πώς συμπεριφέρεται η συνάρτηση όταν το όρισμα πλησιάζει τα οριακά σημεία του τομέα ορισμού, εάν υπάρχουν τέτοια οριακά σημεία. Εάν η συνάρτηση έχει σημεία ασυνέχειας, τότε αυτά τα σημεία ελέγχονται και για την παρουσία κάθετων ασυμπτωμάτων της συνάρτησης. Βρείτε πλάγιες ασύμπτωτες.

4) Να βρείτε τα σημεία τομής της γραφικής παράστασης με τους άξονες συντεταγμένων, που συνίσταται σε έναν απλό υπολογισμό της τιμής της συνάρτησης, με την προϋπόθεση:

Με τον άξονα OX: y=0;

Με άξονα OY: x=0.

Η εύρεση σημείων τομής με τον άξονα μπορεί να οδηγήσει στην ανάγκη επίλυσης μιας σύνθετης αλγεβρικής εξίσωσης, η οποία, ίσως, μπορεί να γίνει μόνο κατά προσέγγιση. Έχοντας βρει τις ρίζες της συνάρτησης και τα σημεία ασυνέχειας, μπορούμε να προσδιορίσουμε το πρόσημο της συνάρτησης σε καθένα από τα διαστήματα μεταξύ αυτών των σημείων. Αυτό μπορεί να γίνει είτε με τον υπολογισμό της τιμής της συνάρτησης σε κάποια από τα σημεία διαστήματος είτε με την εφαρμογή της μεθόδου διαστήματος.

5) Να βρείτε διαστήματα μονοτονίας. Για να το κάνετε αυτό, βρείτε την παράγωγο και λύστε την ανισότητα:

https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, η συνάρτηση μειώνεται.

Έχοντας βρει τα διαστήματα της μονοτονίας, μπορούμε να προσδιορίσουμε αμέσως τα σημεία ενός τοπικού άκρου: όπου η αύξηση αντικαθίσταται από μια μείωση, υπάρχουν τοπικά μέγιστα και όπου η μείωση αντικαθίσταται από μια αύξηση, τοπικά ελάχιστα.

6) Η εύρεση των διαστημάτων κυρτότητας και κοιλότητας πραγματοποιείται χρησιμοποιώντας τη δεύτερη παράγωγο..png" width="39" height="19 src="> στα διαστήματα:

εάν https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, τότε η καμπύλη γραφήματος της συνάρτησης είναι κυρτή.

Ταυτόχρονα, ορίζουμε σημεία καμπής ως εκείνα τα σημεία στα οποία η συνάρτηση αλλάζει την κατεύθυνση της κυρτότητας (και είναι συνεχής).

7) Εύρεση των σημείων τομής της γραφικής παράστασης με την ασύμπτωτη και πρόσθετα σημεία. Αυτό το στοιχείο δεν είναι υποχρεωτικό, αλλά η εύρεση τέτοιων σημείων δίνει τη μελέτη της συνάρτησης και του γραφήματος της που έχει κατασκευαστεί πληρότητα και πληρότητα.

Σημειώστε ότι είναι χρήσιμο να εφαρμόσετε αμέσως τα σημεία στους άξονες συντεταγμένων και στο γράφημα που λήφθηκε κατά τη διαδικασία μελέτης της συνάρτησης στο σχέδιο. Αυτό βοηθά στην κατανόηση της εμφάνισης του γραφήματος στην πορεία.

3. Κάντε το μόνοι σας:

επιλογή	Να βρείτε την παράγωγο της συνάρτησης y:	επιλογή	Να βρείτε την παράγωγο της συνάρτησης y:
	1.y=6-		1.y=-6- 5.y=
	1.y=-7-1		1.y=-7-1
	1.y=4x-3tgx+6x-8		1.y=-5x+2ctgx+3x-2

Στόχοι μαθήματος:

εκπαιδευτικός- γνωρίζει τους τύπους διαφοροποίησης. κανόνες διαφοροποίησης·
διαφοροποίηση μιας σύνθετης συνάρτησης. φυσική και γεωμετρική σημασία της παραγώγου·
την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης.

Εκπαιδευτικός -να μπορεί να βρει παράγωγες συναρτήσεις. επίλυση προβλημάτων χρησιμοποιώντας φυσικό νόημα, γεωμετρικό νόημα. Να βρείτε την τιμή της παραγώγου μιας συνάρτησης σε ένα σημείο. εξηγούν και αιτιολογούν με μαθηματική ικανότητα τις ενέργειες που εκτελούνται.

Εκπαιδευτικός -εκπαιδεύουν την ανεξαρτησία, την ευθύνη, τον προβληματισμό.

Κατά τη διάρκεια των μαθημάτων

Ι. Οργανωτική στιγμή.

II. Έλεγχος εργασιών για το σπίτι
(κατά τη διάρκεια του διαλείμματος, οι σύμβουλοι (φοιτητές) ελέγχουν με βαθμολόγηση).

III. Θέση στόχων και κίνητρο

Ο δάσκαλος ενημερώνει τους μαθητές ότι αυτό το μάθημα είναι το τελευταίο μάθημα με θέμα «Υπολογισμός παραγώγων» και τους καλεί να διατυπώσουν μόνοι τους στόχους.

Δάσκαλος: - «Ο μεγάλος φιλόσοφος Κομφούκιος είπε κάποτε: «Τρία μονοπάτια οδηγούν στη γνώση: το μονοπάτι του προβληματισμού είναι το πιο ευγενές μονοπάτι, το μονοπάτι της μίμησης είναι το πιο εύκολο μονοπάτι και το μονοπάτι της εμπειρίας είναι το πιο πικρό μονοπάτι». Έτσι, σήμερα στο μάθημα, ο καθένας από εσάς θα καθορίσει σε ποιο δρόμο προς τη γνώση αυτού του θέματος βρίσκεται.

Οι μαθητές έχουν την αποστολή να δείξουν τις γνώσεις και τις δεξιότητές τους στον υπολογισμό των παραγώγων και αναφέρεται το σχέδιο μαθήματος.

Στάδιο Ι:Ολοκληρώστε την εργασία στην κάρτα "Απομνημόνευση".
(έλεγχος γνώσεων τύπων και κανόνων διαφοροποίησης).

Στάδιο II:Προφορική μετωπική εργασία για την επανάληψη και τη γενίκευση της γνώσης.

Στάδιο III:"Πρόβλεψη δοκιμής" (κατά την εκτέλεση δοθείσα εργασίαεπιτρέπονται σύμβουλοι).

ΕγώΣτάδιο V:Λύση πρακτικού προβλήματος.

Στάδιο V:Ανεξάρτητη εργασία

I, III, V στάδια εργασίας αξιολογούνται και εργασία για το σπίτι. Οι σύμβουλοι ελέγχουν και καταχωρούν τα αποτελέσματα στον πίνακα αξιολόγησης.

Κριτήρια αξιολόγησης: "5"- 19-20 βαθμοί
"τέσσερα"- 15-18 βαθμοί
"3"- 10-14 βαθμοί.

Μονοπάτια προς τη Γνώση

1. Αναπαραγωγή και διόρθωση βασικών γνώσεων

σκηνοθετώ.

Στόχος:έλεγχος, αυτοέλεγχος γνώσης τύπων και κανόνων διαφοροποίησης

Θυμάμαι! F.I. _________________________________________________
	Παράγωγο
γ, γ - συζ t
	φά"(x)+ σολ"(Χ)
φά(Χ)* σολ(Χ)

Στο τέλος αυτής της εργασίας, πραγματοποιείται αυτοέλεγχος χρησιμοποιώντας τον «Πίνακα παραγώγων». Οι κάρτες παραδίδονται στους συμβούλους για επαλήθευση (δεν επιτρέπονται διορθώσεις στις κάρτες).

V. Γενίκευση και συστηματοποίηση της γνώσης
ΙΙ στάδιο.

1. Προφορική μετωπική εργασία.

ΑΛΛΑ.Διατυπώστε μια εργασία για αυτήν την κατάσταση και λύστε την.

1. Να βρείτε την τιμή της παραγώγου της συνάρτησης στο σημείο t = 3. (Απάντηση: 21.)

2. Γράψτε μια εξίσωση για την εφαπτομένη στη γραφική παράσταση της συνάρτησης στο σημείο t \u003d 3. (Απάντηση: y \u003d 21x-45.).

3. Να βρείτε την ταχύτητα και την επιτάχυνση του σώματος τη χρονική στιγμή t=3c αν ο νόμος της κίνησης δίνεται από τον τύπο . (Απάντηση: 21m/s, 16m/s²).

4. Να βρείτε την κλίση της εφαπτομένης που σχεδιάζεται στη γραφική παράσταση της συνάρτησης στο σημείο t = 3. (Απάντηση: 21.).

5. Βρείτε την εφαπτομένη της κλίσης της εφαπτομένης στη γραφική παράσταση της συνάρτησης στο σημείο t = 3 και προσδιορίστε το είδος της γωνίας μεταξύ της εφαπτομένης και της θετικής κατεύθυνσης του άξονα Ox. (Απάντηση: tgα, η γωνία α είναι οξεία)

Β. Να βρείτε παραγώγους συναρτήσεων

2. Στάδιο III«Πρόβλεψη δοκιμής»

Στο τέλος αυτής της εργασίας, γίνεται αυτοέλεγχος με βάση τις τελικές απαντήσεις και τα τεστ παραδίδονται σε συμβούλους. (δεν επιτρέπεται η διόρθωση σε κάρτες).
Απαντήσεις:

1 επιλογή
Επιλογή 2

1. Η λύση του προβλήματος

ΕγώΣτάδιο V
Μετωπική επίλυση του προβλήματος αυξημένου επιπέδου (η λύση εκτελείται από συμβούλους μαζί με την τάξη).

Μια εργασία

Σε ποια τιμή της παραμέτρου έναεφαπτομένη στη γραφική παράσταση της συνάρτησης

τραβηγμένο στα σημεία τομής του με τον άξονα Χ σχηματίζουν γωνία 60°;

Η γραφική παράσταση είναι μια παραβολή με ανοδικούς κλάδους που τέμνουν τον άξονα x σε δύο σημεία (η περίπτωση έναΤο =0 δεν ικανοποιεί την έννοια του προβλήματος):

IX. Σύνοψη και βαθμολόγηση

1. Ερωτήσεις: α) Επιτεύχθηκε ο στόχος του μαθήματος;
β) Ποιο στάδιο φάνηκε το πιο δύσκολο;
γ) Ποιο ήταν το πιο ενδιαφέρον;

2. Οι σύμβουλοι ανακοινώνουν τα αποτελέσματα (αριθμός και επώνυμο των μαθητών καθ' οδόν
μίμηση, τρόποι προβληματισμού και τρόποι εμπειρίας).