Drainage

Imre Lakatos. Methodology of research programs

Date of death: Citizenship:

Great Britain

School/tradition:

critical rationalism

Direction: Influenced:

Imre Lakatos(in Hungarian Lakatosh- hung. Lakatos Imre real name and surname Avrum Lipschitz; November 9, Debrecen - February 2, London) - an English philosopher of Hungarian origin, one of the representatives of postpositivism.

Biography

Methodology of research programs

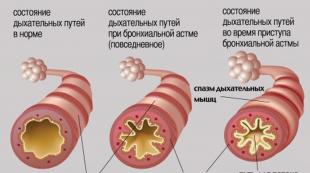
Lakatos described science as a competitive struggle of "research programs" consisting of "hard core" a priori accepted in the system of fundamental assumptions that cannot be refuted within the program, and "safety belt" auxiliary hypotheses ad hoc , modified and adapted to the counterexamples of the program. The evolution of a specific program occurs due to the modification and refinement of the "safety belt", while the destruction of the "hard core" theoretically means the cancellation of the program and its replacement with another, competing one.

The main criterion for the scientific nature of the program Lakatos calls the increase in factual knowledge due to its predictive power. While the program gives an increase in knowledge, the work of a scientist within its framework "rational". When the program loses its predictive power and begins to work only on the "belt" of auxiliary hypotheses, Lakatos prescribes to abandon its further development. However, it is pointed out that in some cases the research program experiences its own internal crisis and again gives scientific results; thus, the "loyalty" of the scientist to the chosen program, even in times of crisis, is recognized by Lakatos "rational".

Method of rational reconstructions

The method of rational reconstructions of the history of science is applied by Lakatos in the book Evidence and refutation to the history of the proofs of the Descartes-Euler-Cauchy theorem on the relationship between the number of vertices, edges and faces of an arbitrary polyhedron. At the same time, in the footnotes, Lakatos gives a broader picture of the history of mathematics, especially the history of calculus and mathematics foundation programs in the 19th and early 20th centuries. Lakatos discusses the history of mathematics as a chain in which

“Checking an ordinary proof is often a very delicate undertaking, and it takes as much intuition and happiness to attack a 'mistake' as it does to stumble upon a proof; discovering "errors" in informal proofs can sometimes take decades, if not centuries. Informal quasi-empirical mathematics does not develop as a monotonous increase in the number of undeniably proved theorems, but only through the continuous improvement of conjectures through reflection and criticism, through the logic of proofs and refutations.

The book itself is not written in the form of a historical study, but in the form of a school dialogue. Using the dialogical method, Lakatos artificially constructs a problematic situation in which the concept of the "Eulerian polyhedron" is formed. Rational reconstruction by Lakatos does not reproduce all the details real history, but is created specifically for the purpose of rationally explaining the development of scientific knowledge.

Literature

Compositions

Lakatos I. Evidence and refutation. How theorems are proved. Per. I. N. Veselovsky.- M.: Nauka, 1967.
Lakatos I. Falsification and methodology of research programs .- M .: Medium, 1995.
Lakatos I. History of Science and Its Rational Reconstructions // App. to the book: Kuhn T. The structure of scientific revolutions. - M.: AST, 2001.
Lakatos I. Selected works on the philosophy and methodology of science. - M .: Academic Project, 2008.
Lakatos I. Science and Pseudoscience. (Speech on the radio program of the Open University June 30, 1973)

About Lakatos

Bandy A. chocolate and chess. Unlocking Lakatos. Budapest: Akademiai Kiado, 2010.
Kadvany J. Imre Lakatos and the guises of reason. Durham and London: Duke University Press, 2001.
Koetsier T. Lakatos" philosophy of mathematics: a historical approach. Amsterdam e.o.: North Holland, 1991.
Larvor B. Lakatos: an introduction. London: Routledge, 1998.
Long J. Lakatos in Hungary. Philosophy of the social sciences, 28, 1998, pp. 244-311.

Lakatos filled with new content the principle of falsification and ionism as the methodological basis of the theory of scientific rationality. According to this principle, rationality scientific activity is confirmed by the willingness of a scientist to recognize any scientific hypothesis as refuted when it encounters experience that contradicts it (not only to recognize, but also to strive for possible refutation of his own hypotheses).

Lakatos wrote small, but very capacious works. You can get acquainted with his views in the books published in Russian "Proofs and Refutations" (M., 1967) and "Falsification and Methodology of Research Programs" (M., 1995).

In his early works (of which the most famous is Proofs and Refutations), Lakatos proposed a variant of the logic of conjectures and refutations, applying it as a rational reconstruction of the development of knowledge in mathematics in the 17th-19th centuries. Already during this period, he clearly stated that "the dogmas of logical positivism are disastrous for the history and philosophy of mathematics."

The line of analysis of the processes of change and development of knowledge is then continued by the philosopher in a series of his articles and monographs, which set out a universal concept of the development of science, based on the idea of competing research programs.

1. Falsificationism as a methodological basis for the theory of scientific rationality

Falsificationism combined the postulates of empiricism and rationality: rationality is based on the universalization of empiricism, and empiricism is adequately embodied in the criterion of rationality. Lakatos extended this connection to the realm of developing mathematics. In terms of its rational structure, the path of scientific research in mathematics is the same as in empirical natural science: the discovered "counterexamples" force the researcher to modify the hypotheses put forward, improve the evidence, use the heuristic potential of the accepted assumptions, or put forward new ones. However, in both mathematics and empirical science, the rationality of criticism does not mean a requirement for the immediate rejection of refuted hypotheses.

In the overwhelming majority of cases, the rational behavior of the researcher contains a number of intellectual strategies, the general meaning of which is to move forward without stopping because of individual failures, if the movement promises new successes and these promises come true. This is evidenced by the history of science, which thus comes into conflict with dogmatic falsificationism.

Science, according to Lakatos, is and should be a competition between competing research programs. It is this idea that characterizes the so-called refined methodological falsificationism developed by Lakatos in line with Popper's concept. Lakatos tries to soften the sharpest corners of Popper's philosophy of science. He distinguishes three stages in the development of Popper's views: Popper - dogmatic falsificationism, Popper - naive falsificationism, Popper - methodological falsificationism. The last period begins in the 50s and is associated with the development of a normative concept of the growth and development of knowledge based on comprehensive criticism.

Lakatos saw well the shortcomings of Popper's methodology. The strict methodological requirement that a theory must be abandoned if it turned out to be falsified sharply diverged from the real activities of scientists who continued to work with such a theory, tried to improve it, and even often achieved success.

Popper's concept could not explain such facts from the history of science. Many scientific theories, faced with facts that disprove them, remain in the scientific community for a long time, they are used and applied. Moreover, if new theories appear in science that have successfully coped with the anomalies of their predecessors, then competing theories continue to coexist.

But, of course, Lakatos was not a simple apprentice of a great master and teacher. He calls Popper's original version of methodology "naive falsificationism". Many followers of Popper tried to connect his concept with the history of science, to confirm it with historical facts. The desire to give a rational reconstruction of the history of science leads Lakatos to an independent version of critical rationalism.

Methodological falsificationism corrects the error of the dogmatists, showing the fragility of the empirical base of science and the means of hypothesis control it offers (this is shown by Popper in " The logic of scientific discovery).However, Lakatos continues, methodological falsificationism is not enough. The picture of scientific knowledge presented as a series of duels between theory and facts is not entirely correct. In the struggle between the theoretical and the actual, Lakatos believes, there are at least three participants: facts and two competing theories. It becomes clear that a theory becomes obsolete not when a fact that contradicts it is announced, but when a theory that is better than the previous one declares itself. Thus, Newtonian mechanics became a fact of the past only after the advent of Einstein's theory.

In an effort to somehow mitigate the extremes of methodological falsificationism, I. Lakatos put forward the concept of research programs as a weakening mechanism of evolutionary epistemology.

2. Methodology of research programs by Imre Lakatos

In order to bring the methodological concept closer to real historical practice, Lakatos introduces a new concept of "research program" or "research program" into the methodology of science. If Popper and the logical positivists use in their reasoning the concept of "theory" or "set of theories" as the initial and main cell of analysis, then Lakatos' methodological analysis unit is the "research program". In the understanding of Lakatos, this is a set of theories accepted sequentially one after another in time and coexisting together. All these theories belong to the same program, because they have a common beginning: they have fundamental ideas and principles that unite them.

Lakatos also assumes that in the history of science there are several parallel research programs related to the same subject of research, solving approximately similar problems and being in relation to each other in a competitive struggle. Such programs can coexist for quite a long time, the victory of one of them comes gradually, and the significance of this victory can be assessed, including with the help of the defeated program, in comparison with those problems that cannot be solved by the latter.

The research program is structurally composed of three main elements: the core of the program, positive and negative heuristics.

The core of the research program is a rigid, unchanging part of the research program, consisting of a set of fundamental theoretical principles, specific scientific and metaphysical assumptions about the ontological nature of the area under study and the general strategy for its study. During the entire lifetime of the program, its core does not change.

Positive heuristics, being the second essential part of the research program, “identifies problems for research, highlights the protective belt of auxiliary hypotheses, anticipates anomalies and victoriously turns them into confirming examples - all this in accordance with a predetermined plan. The scientist sees anomalies, but, since his research the program can withstand their onslaught, he can freely ignore them. Not anomalies, but the positive heuristics of his program - that's what his choice of problems dictates in the first place. The fulfillment of such requirements entails a significant change in theories. Scientists are forced to take measures to explain counterexamples, when it is no longer possible to ignore them in a competitive struggle with other research programs, and to improve their theories. Positive heuristics is turning into the main driving force of science. Let us note that for Popper, changing falsified theories is tantamount to a rejection of falsification and was, in fact, a regressive phenomenon, a loophole for dogmatism.

Negative heuristics are a set of techniques and rules that are designed to protect the core of the program from empirical rebuttals. This position is also significantly different from Popper's methodology, which forbade formulating and consciously putting forward techniques that prevent the falsification of theories. Popper defended this methodological requirement under outwardly attractive slogans: "Down with dogmatism from science!" and "Criticism is the driving force of scientific progress!" . But the whole point is that these beautiful slogans turned out to be empty words and good wishes in the face of historical facts. Lakatos, formulating the principles of negative heuristics, tries to bring the methodological conception into line with the real history of science.

As for the auxiliary hypotheses, which are formulated based on the general strategy of positive and negative heuristics, they are a changing part of the research program and are intended to protect both the core of the program and theories. Moreover, each of the theories of the research program has its own protective belt of auxiliary hypotheses.

The research program practically exists and is implemented as a series of theories that arise sequentially in time and have the ability to exist in parallel for some time. If some of them lose support from heuristics and even their own protective belts, then the program as a whole can be saved at the expense of the core and the remaining unfalsified theories.

In the history of science, several research programs coexist and compete with each other. How to determine which of them with greater reliability and evidence can achieve success? And what program will determine the progressive development of science? The main problem in this respect is the problem of defining criteria for the success of a research program. Lakatos believes that this criterion is the heuristic value of the research program. Theoretical predictions of new facts must outstrip their empirical confirmation.

critical rationalism lakatos falsificationism

"A research program," wrote Lakatos, "is said to be progressing when its theoretical growth anticipates its empirical growth, i.e., when it can predict new facts with some success ("progressive problem shift"); a program regresses if its theoretical growth lags behind its empirical growth, i.e. when it gives only belated explanations of either random facts or facts anticipated and discovered by a competing program ("regressive problem shift").

If a research program progressively explains more than a competing one, then it "crowds out" it, and that competing program can be eliminated (or, if you prefer, "delayed"). So, the more successful research program is the one that produces more new predictions that are confirmed by experience. Such a program is more progressive. Experience acts as a measure in the evaluation of competing programs. If the experience refutes the theory, then the entire research program, while retaining the core and positive heuristics, remains viable.

The refutation of a theory is not a basis for its rejection, much less for the rejection of the entire program. From Lakatos's point of view, there is no such thing as a decisive experiment, which is usually incorrectly associated with the collapse of a theory, in science. "Thus, for example, in one place Popper claims that the Michelson-Morley experiment decisively subverted the classical theory of the ether; in another place he exaggerates the role of this experiment in the emergence of Einstein's theory of relativity. One must really put on all the simplifying glasses of a naive falsificationist in order to see together with Popper, that Lavoisier's classical experiments disproved (or "sought to disprove") the phlogiston theory, that the Bohr-Kramers-Slater theory was blown to smithereens by a whiff of Compton's research, or that the parity principle was "abandoned" by a "counterexample".

Denying the possibility of a decisive experiment, Lakatos tries to restore historical justice by proving that in addition to "stubborn" facts (moreover, still incorrectly interpreted), living people act in science, who very often act contrary to these facts.

Lakatos's rational reconstruction of the history of science is much closer to real scientific activity than the methodology of logical positivism and Popper's abstract falsificationism.

3. Formalism in science

Lakatos contrasts the latter (as the essence of logical positivism) with a program for analyzing the development of meaningful mathematics, based on the unity of the logic of proofs and refutations. This analysis is nothing but a logical reconstruction of the real historical process of scientific knowledge.

I. Lakatos writes that it often happens in the history of thought that when a new powerful method appears, the study of problems that can be solved by this method quickly comes to the fore, while all the others are ignored, even forgotten, and its study is neglected.

He argues that this is what seems to have happened in our century in the field of the philosophy of mathematics as a result of its rapid development.

The subject of mathematics consists in such an abstraction of mathematics when mathematical theories are replaced by formal systems, proofs by some sequences of well-known formulas, definitions by "abbreviated expressions that are "theoretically optional, but typographically convenient".

Such an abstraction was invented by Hilbert in order to obtain a powerful technique for studying the problems of the methodology of mathematics. But at the same time, I. Lakatos notes that there are problems that fall outside the framework of mathematical abstraction. Among them are all problems related to "meaningful" mathematics and its development, and all problems related to situational logic and decision math problems. The term "situational logic" belongs to Popper. This term denotes productive logic, the logic of mathematical creativity.

The school of mathematical philosophy, which seeks to identify mathematics with its mathematical abstraction (and the philosophy of mathematics with metamathematics), I. Lakatos calls the "formalist" school. One of the clearest characteristics of the formalist position is found in Carnap. Carnap requires that:

a) philosophy was replaced by the logic of science., but

b) the logic of science is nothing but the logical syntax of the language of science.,

c) mathematics is the syntax of a mathematical language.

Those. the philosophy of mathematics should be replaced by metamathematics.

Formalism, according to I. Lakatos, separates the history of mathematics from the philosophy of mathematics; in fact, the history of mathematics does not exist. Any Formalist must agree with Russell's remark that Boole's Laws of Thought (Boole, 1854) was "the first book ever written on mathematics. Formalism denies the status of mathematics for most of what is usually understood to be included in mathematics, and nothing cannot speak of its “development.” “None of the “critical” periods of mathematical theories can be admitted into the formalistic sky, where mathematical theories dwell like seraphim, cleansed of all stains of earthly unreliability. However, formalists usually leave a small back door open for fallen angels; if for some "mixtures of mathematics and something else" it turns out to be possible to construct formal systems "which in some sense include them", then they can then be admitted.

Under the current dominance of formalism, I. Lakatos paraphrases Kant: the history of mathematics, having lost the guidance of philosophy, has become blind, while the philosophy of mathematics, turning its back on the most intriguing events in the history of mathematics, has become empty.

According to Lakatos, "formalism" provides a fortress for logical positivist philosophy. According to logical positivism, a statement only makes sense if it is "tautological" or empirical. Since meaningful mathematics is neither "tautological" nor empirical, it must be meaningless, it is pure nonsense. Here he pushes back from Turquette, who argues with Kopi that Gödel's propositions make no sense. Kopi believes that these provisions are "a priori truths", but not analytic, they refute the analytic theory of a priori.

Lakatos noted that none of them noticed that the special status of Gödel's propositions from this point of view is that these theorems are theorems of informal meaningful mathematics, and that in fact they both discuss the status of informal mathematics in a particular case. The theories of informal mathematics are definitely guesses that can hardly be divided into a priori and a posteriori. That. the dogmas of logical positivism are disastrous for the history and philosophy of mathematics.

I. Lakatos, in the expression methodology of science, uses the word "methodology" in a sense close to the "heuristics" of Paul and Bernays and to Popper's "logic of discovery" or "situational logic". Removing the term "methodology of mathematics" to be used as a synonym for "metamathematics" has a formalistic flavor. This shows that there is no real place in the formalist philosophy of mathematics for methodology as the logic of discovery. Formalists believe that mathematics is identical to formalized mathematics.

He argues that two sets of things can be discovered in a formalized theory:

It is possible to discover the solution of problems that a Turing machine (it is a finite list of rules or a finite description of a procedure in our intuitive understanding of the algorithm) with the right program can solve in a finite time. But no mathematician is interested in following this boring mechanical "method" prescribed by the procedures for such a solution.

One can find solutions to problems like: whether or not some formula of a theory will be a theorem, in which the possibility of a final solution has not been established, where one can be guided only by the "method" of unguided intuition and luck.

According to I. Lakatos, this gloomy alternative to machine rationalism and irrational blind guessing is unsuitable for living mathematics. The researcher of informal mathematics gives creative mathematicians a rich situational logic that will be neither mechanical nor irrational, but which cannot in any way be recognized and encouraged by formalist philosophy.

But all the same, he admits that the history of mathematics and the logic of mathematical discovery, i.e. phylogenesis and ontogeny of mathematical thought cannot be developed without criticism and the final rejection of formalism.

Thus, the purpose of this book by I. Lakatos is a challenge to mathematical formalism.

Conclusion

Lakatos is one of the most prominent representatives of "critical rationalism".

Lakatos filled with new content the principle of falsificationism as a methodological basis for the theory of scientific rationality. According to this principle, the rationality of scientific activity is confirmed by the readiness of a scientist to recognize any scientific hypothesis as refuted when it encounters experience that contradicts it (not only to recognize, but also to strive for possible refutation of his own hypotheses).

Lakatos made an attempt to combine a historical approach to science with the preservation of a rationalist attitude. This was expressed in the methodological concept of "refined falsificationism" developed by him, which is more often called the methodology of research programs. The rational development of science is presented in this concept as a rivalry of "conceptual systems", the elements of which can be not only individual concepts and judgments, but also complex complexes of dynamically developing theories, research projects and their relationships.

Lakatos was looking for the possibility of moving towards the history of science on the basis of rationalism. The methodology of Lakatos is the most important tool for the rational analysis of science, one of the most significant achievements of the methodology of science in the 20th century.

I. Lakatos pays attention to the problem of scientific formalism and traces it on the basis of the philosophy of mathematics, as the closest direction in the philosophy of science. According to Lakatos, "formalism" provides a fortress for logical positivist philosophy, this gloomy alternative to machine rationalism and irrational blind guessing is unsuitable for living mathematics.

List of used literature

1.Lakatos I. Proofs and rebuttals. - M., 1967. - 152 p.

2.Lakatos I. History of science and its rational reconstructions. - M., 1978. - 235s.

.Lakatos I. Methodology of scientific research programs // Questions of Philosophy. - 1995. - No. 4.

.Lakatos I. Falsification and methodology of research programs. M., 1995.

.Gubin V.D. etc. Philosophy. - M., 1997. - 432s.

.Radugin A.A. Philosophy. Lecture course. - M., 1995. - 304 p.

.Rakitov A.I. Philosophical problems of science. - M.; 1977. - 270s.

.Reale D. Western philosophy from the origins to the present day. Part 4 / Giovanni Reale, Dario Antiseri. - L., 1997.

.Sokolov A.N. The subject of philosophy and the rationale for science. - S. P.; 1993. - 160s.

.Philosophy: textbook / ed. A.F. Zotova, V.V. Mironova, A.V. Razin. - 6th ed., revised. and additional - M.: Academic Project, 2009. - 688 p.

.Philosophy and methodology of science. Part 1. - M.; 1994. - 304p.

.Philosophy and methodology of science. Part 2. - M.; 1994. - 200s.

Regular revised article

Imre Lakatos
hung. Imre Lakatos
Imre Lakatos Imre Lakatos
Date of Birth:
Place of Birth:	Debrecen
Date of death:
A place of death:

Imre Lakatos(in Hungarian Lakatosh- hung. Imre Lakatos, real name and surname Avrum Liposhits; November 9, 1922, Debrecen - February 2, 1974, London) - English philosopher of science of Hungarian origin.

Biography

Sharing Popper's belief in a universal criterion of scientific rationality, in contrast to his contemporaries T. S. Kuhn and M. Polanyi, Lakatos developed Popper's proposed methodological research program with more emphasis on rationally reconstructed history using concrete examples. According to Lakatos, “The philosophy of science without the history of science is empty; the history of science without philosophy is blind.”

Philosophy of Science

The main achievement of Lakatos in the philosophy of science is the postulation of research programs as a key to understanding the progress of theoretical science. Unlike Popper, who believed that the criterion of falsifiability applied to individual theories, Lakatos considered research programs that included a series of theories and contained both falsifiable and non-falsifiable elements, more suitable for assessing the durability of scientific theories and the rationality of their rejection.

Lakatos described science as a competitive struggle of "research programs" consisting of "hard core" a priori accepted in the system of fundamental assumptions that cannot be refuted within the program, and "safety belt" auxiliary hypotheses ad hoc, modified and adapted to the counterexamples of the program. The evolution of a specific program occurs due to the modification and refinement of the "safety belt", while the destruction of the "hard core" theoretically means the cancellation of the program and its replacement with another, competing one.

Method of rational reconstructions

“Checking an ordinary proof is often a very delicate undertaking, and it takes as much intuition and happiness to attack a 'mistake' as it does to stumble upon a proof; discovering "errors" in informal proofs can sometimes take decades, if not centuries. Informal quasi-empirical mathematics does not develop as a monotonous increase in the number of undeniably proved theorems, but only through the continuous improvement of conjectures through reflection and criticism, through the logic of proofs and refutations.

The book itself is not written in the form of a historical study, but in the form of a school dialogue. Using the dialogical method, Lakatos artificially constructs a problematic situation in which the concept of the "Eulerian polyhedron" is formed. Rational reconstruction by Lakatos does not reproduce all the details of real history, but is created specifically for the purpose of rationally explaining the development of scientific knowledge.

The attitude of philosophers and scientists to the ideas of Lakatos was ambiguous. Despite the objections of some of them, Lakatos' research programs have become part of the modern philosophy of science.

Major works of Lakatos

"Proofs and rebuttals: the logic of mathematical discoveries" (1976) "Philosophical articles" (vol. 1 - "Methodology of research programs", vol. 2 - "Mathematics, science and epistemology", 1978).

Links to essays

Lakatos I. Proofs and rebuttals. How theorems are proved. Per. I. N. Veselovsky. Moscow: Nauka, 1967.
Lakatos I. Falsification and Methodology of Research Programs. M.: Medium, 1995.
Lakatos I. History of science and its rational reconstructions // Pril. to the book: Kuhn T. The structure of scientific revolutions. M.: AST, 2001.

ca:Imre Lakatos cs:Imre Lakatosfa:ایمره لااتوش fi:Imre Lakatoshr:Imre Lakatos hu:Lakatos Imrenl:Imre Lakatos no:Imre Lakatos pl:Imre Lakatos pt:Imre Lakatos ro:Imre Lakatos sk:I :Imre Lakatos Notification: The preliminary basis for this article was a similar article in http://ru.wikipedia.org , under the terms of CC-BY-SA, http://creativecommons.org/licenses/by-sa/3.0 , which was subsequently changed, corrected and edited.

Notification: The preliminary basis for this article was the article

Knowledge is that which is evidence-based. However, there is criticism (of what we can all justify with the help of intellect and feelings). The history of scientific theory has continuity - the development of a certain research program. As an initial model for the growth of scientific knowledge, Lakatos takes the world of ideas, autonomously developing knowledge, in which the "internal history" of knowledge is realized. However, while according to Popper, one theory is replaced by another, the old theory is completely rejected, according to Lakatos, the growth of knowledge takes place in the form of a critical dialogue of competing research programs. It is they, and not theories, that are the fundamental unit of the development of science.

Research program is realized in a historically evolving sequence of theories, each of which arises from the previous one by modification caused by the encounter with experimental counterexamples that contradict it. The “hard core” of a program moves from one theory of a given program to another, and the protective belt, consisting of auxiliary hypotheses, can be partially destroyed.

The main value of the program is its ability to replenish knowledge and predict new facts. Contradictions and difficulties in explaining any phenomena do not significantly affect the attitude of scientists towards it (which is actually happening!). Indeed, an idea that is theoretically strong enough always turns out to be rich enough to be defended. Only when the "hard core" of the program is destroyed will a transition from the old research program to the new one become necessary. This is the essence of the "scientific revolution".

In modern Western philosophy, the problem of the growth and development of knowledge is central. The problem was especially actively developed by supporters of post-positivism - Popper, Kuhn, Lakatos and others.

Following Popper, Lakatos believes that the basis of the theory of scientific rationality should be principle of criticism. This principle is universal; however, "rational criticism" should not be reduced to a demand for ruthless falsification. Anomalies should not encourage scientists to crack down on their theories; the rational behavior of the researcher is to move forward, not numb from individual failures, if this movement promises new successes.

In Lakatos, it is not two theories that are compared and evaluated, as in Popper's, but a series of them, defined as a research program. The development of science is "the history of the birth, life and death of research programs."

Basic principle of Lakatos is a combination of philosophy and the history of science. In this regard, he formulates an important proposition: “The philosophy of science without the history of science is empty; the history of science without the philosophy of science is blind.” Therefore, he developed the theory of "research programs".

Research program is a set of theories developing on the basis of common research and methodological principles. Structurally includes:
1) "hard core" - the fundamental principles of all theories of the program, helping to maintain its integrity; 2) "protective belt" - auxiliary hypotheses of the program; it ensures the safety of the "hard core". The protective belt must adapt and remake under the pressure of new facts; 3) methodological principles that determine the prospects for the application of this program - "positive" and "negative heuristics".

« Negative Heuristic”is a restriction in the form of rules to avoid false paths of knowledge. "Negative heuristic" defines the "hard core" of the program, considered "irrefutable". " Positive heuristic" is a set of rules that allow you to modify the program in such a way as to save it or improve it. "Positive heuristics" consists of arguments more or less clear, and assumptions more or less probable, aimed at changing and developing the research program.

The evolution of a specific program occurs due to the modification and refinement of the "safety belt", while the destruction of the "hard core" means the cancellation of the program and its replacement by a competing one.

The main criterion for the scientific nature of the program is the growth of knowledge. While the program gives an increase in knowledge ( progressive program), the work of a scientist within its framework is “rational”. When the program loses its predictive power and works only on auxiliary hypotheses, Lakatos prescribes to abandon it ( regressive program).

Unlike Kuhn, Lakatos suggests that periods of "normal science" when a single research program dominates are extremely rare. And that Kuhn's "paradigm" is the research program that temporarily seized the monopoly. More often there are periods when there are many research programs and they compete with each other. But science doesn't have to be "normal" because the sooner the rivalry starts, the better it is for progress. The theory is never falsified, but replaced by a better one. The strength of a research program is determined by heuristic strength, which refers to the ability of the program to theoretically predict the emergence of new facts.

Lakatos further distinguishes two main types of science: mature science» is a type of science where research programs compete. It consists of research programs that not only explain unknown facts but also anticipating new theories. Only mature science has "heuristic power"; " Immature Science» is a type of science where research is carried out according to a model.

Changing the main research programs is scientific revolution. According to Lakatos, there have been 3 scientific revolutions, the result of which was a consistent change in inductivism, conventionalism and the methodology of research programs. But this occurrence is rare. If some experiment shows that the program does not work, then it needs to be replaced. But if, after some time, another scientist explains that experiment in terms of an "outdated program", then this program will be restored again. An example, Darwin's theory and "Jenkins' nightmare".

Thus, from the concept of Lakatos it is clear that scientific revolutions do not play a very significant role. In science, there are almost never periods of undivided domination of one "program", because there is competition between different programs.

Shifts or minor change - all these estimates are made only retrospectively. According to Lakatos, the history of science is the judge of any concept.

The philosophical concept of I. Lakatos was formed under the influence of the teachings of K. Popper. In many respects sharing the position of the latter, Lakatos believes (although he does not explicitly say so anywhere) that Popper's doctrine needs substantial addition. It is about the following. Having proposed the principle of falsification, Popper, according to Lakatos, did not take care to develop mechanism falsification. And the absence of such a mechanism can negate the very fruitful idea of falsification.

In his work Methodology of Research Programs, Lakatos draws the reader's attention to the fact that no scientific theory arises simultaneously (the same can be attributed to any fundamental principle that unites several theories around itself). In the process of its formation, the theory goes through several stages. A theory (or set of interrelated theories) in development is what Lakatos calls a "research program." A scientific research program is a sequence characterized by "continuity, connecting ... elements into a single whole".

Since it is customary in our textbook to use the terms "empiricism" and "theory", in order not to introduce additional difficulties, we will not deviate from this tradition - and we will replace the Lakatosian term "program" in our presentation with the term "theory", bearing in mind that Lakatos is primarily interested in theory as a living, developing organism.

Suppose that any scientific theory can be written down as economically as possible. This means that it is possible to formulate such a series of interrelated statements and formulas that will clearly express the main idea of this theory. For example, Newtonian mechanics in its brief formulation consists of the law of universal gravitation and three laws of dynamics. Such a summary of the theory, in the terminology of Lakatos, is called solid core theory.

The core of the theory must be treated with the utmost care; under no circumstances make the slightest change to it. This means that no matter what new facts are discovered in that area of nature or society, the explanation of which this theory claims, the core cannot be replaced in any case. For such prohibition of changing the kernel, Lakatos introduces a special term - negative heuristics. The negative heuristic is a kind of "protective belt" around the kernel.

But if the essence of the theory cannot be changed, then how should the theory react to emerging circumstances that do not fully agree with it (internal contradictions of the theory, facts that contradict it)? The theory must have the so-called positive heuristics, i.e. it must be able to develop auxiliary hypotheses that can transform the content of the theory in such a way that the core remains unchanged, and new facts organically enter the empirical basis of this theory. For example, for a schema solar system, proposed by N. Copernicus, where the "core" is the idea of planetary rotation around the Sun, are quite acceptable various options trajectories of the planets. It was this circumstance that allowed I. Kepler, having made some changes in the theory of Copernicus (known to us as Kepler's laws) and without affecting its core, to give the heliocentric system a logically harmonious and scientifically substantiated form. Thus, positive heuristics are the possibilities of its modification, provided in advance in the theory, which are safe for the integrity of the solid core of the theory.

In general, the research program looks like this (Fig. 2.2):

1) the solid core of the theory - a brief formulation of its main ideas;
2) negative heuristics - a ban on changing the core of the theory;
3) positive heuristics - the possibility of such changes in the theory that will not affect its core.

Rice. 2.2. Structure of the research program

Everything that has been said so far looks somewhat paradoxical in the light of Lakatos' main intention - to develop a mechanism for falsifying a theory. While the mechanism of its infinite preservation turns out.

But the whole point is that this is not yet the actual mechanism for changing theories, but rather the clarification and systematization of the real process of formation and the mode of existence of a scientific theory. Very often, a scientist (or a team of scientists) who has created a new concept defends its main idea in every possible way, correcting, if necessary, its peripheral areas. Lakatos formulates the features of the scientific process in a rational way, implicitly believing that science develops precisely “programmatically” and nothing needs to be changed here (and it is impossible), but only these rules need to be clearly understood and observed. You also need to be aware of the fact that "voluntarily" theory does not "cancel" itself.

A theory can only be replaced by another theory, formulated independently of the first one, a competing theory.

What requirements should the competitor theory (hereinafter - T2) meet?

1. T2 must have a solid core absolutely different from the first theory (hereinafter - Tx).
2. T2 must have a negative heuristic (the negative heuristic is the same for all theories).
3. T2 must have a positive heuristic other than that of G.
4. T2 should explain all the facts that T1 unable to explain (i.e. T2 should have a more powerful empirical base than Gj).
5. T2 should predict all those facts that G1 predicts, and, in addition, predict facts (or indicate the direction of their search) that G cannot predict (i.e. T2 should have more powerful heuristic power).

If the requirements listed in these five points are met, then T2 replaces T1 and becomes the leading theory in a certain field of knowledge.

Now let's return to the question posed at the beginning of the conversation about Lakatos: how is the theory falsified? The answer will be this: the theory is falsified by facts that do not contradict it (there is no such fact that the theory could not "digest"), but another a theory that offers a different conception of reality and is supported by a large set of facts, and this set (as part of it) includes facts that support the falsifiable theory.